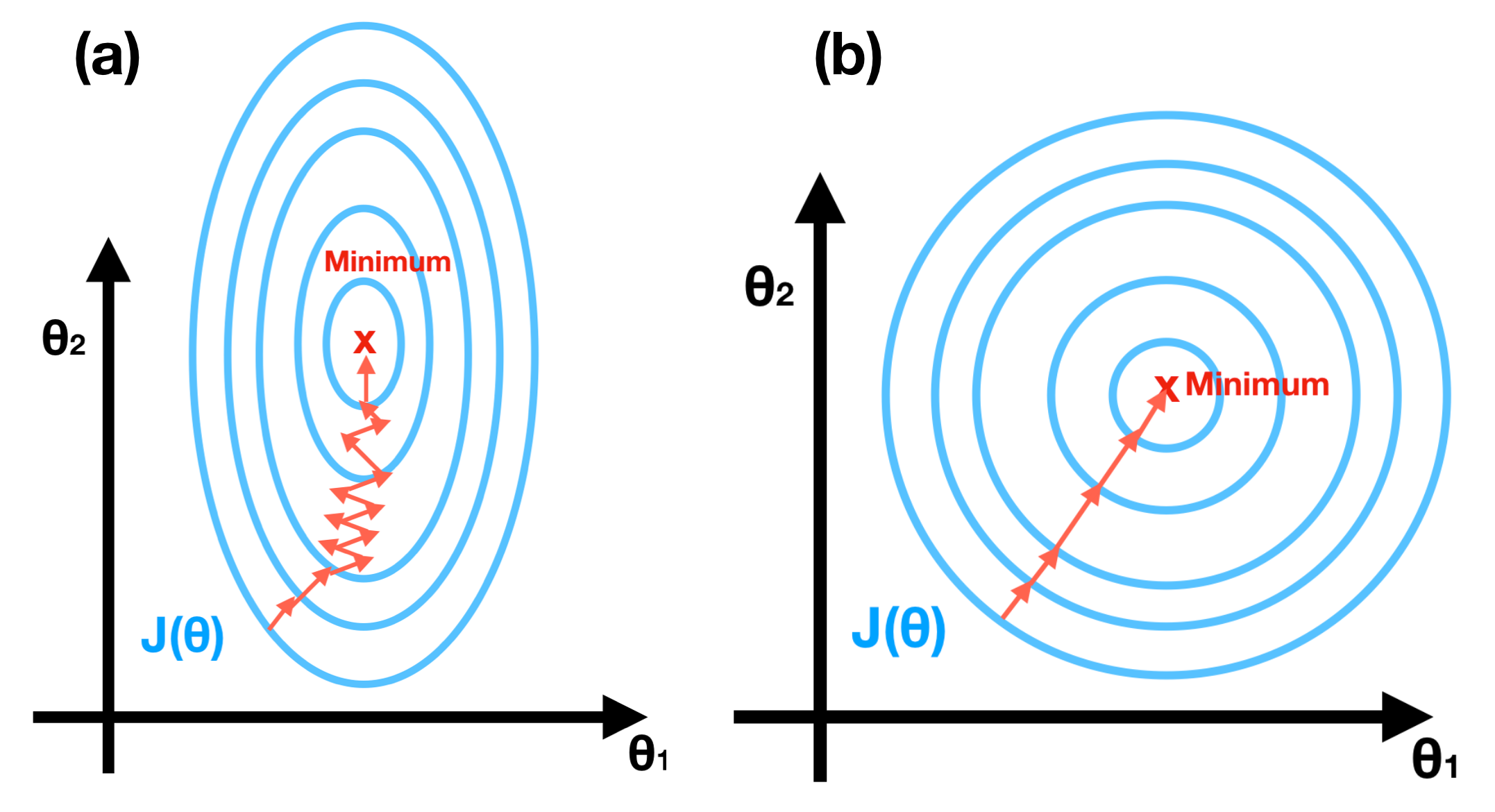
Below we mention the most important problem of the SGD method for optimization.
if the ratio of largest to smallest in the hessian matrix is high, the learning rate could become much lower. Because of oscillation along the axis with a high gradient.

The gradient in local minima or saddle point is zero, so SGD gets stuck and can't find the optimal point.
In the SGD, we calculate the gradient in mini-batches, which approximates the gradient on training data, not the exact one. It could raise the number of iterations for convergence.

In SGD + Momentum, we suppose the gradient as acceleration, not velocity.
$$ v_0 = 0 \\v_{t+1} = \rho v_t + \nabla f(x_t)\\ x_{t+1} = x_t - \alpha v_{t+1} $$
This new approach could help to solve all the problems we talk about it above.
$$ v_0 = 0 \\v_{t+1} = \rho v_t - \alpha \nabla f(x_t + \rho v_t)\\ x_{t+1} = x_t + v_{t+1} $$